Ak ste niekedy hádzali mincou, tak viete, že máte rovnakú šancu, či vám padne jedna alebo druhá strana. Častokrát sa však stane, že vám padne aj tri-štyrikrát za sebou jedna a tá istá strana mince. Znamená to, že šance neboli predsa len rovnaké? Prečo je to tak a ako chápať tú 50-percentnú pravdepodobnosť, či padne jedna alebo druhá strana?
Rozhodnutia robíme každodenne celý svoj život. Či prebehnúť cez cestu, či si kúpiť auto, či zariskovať, či ísť na vysokú školu, či teraz investovať na finančných trhoch a mnohé ďalšie.
Pri chápaní pravdepodobnosti výskytu určitého javu sa častokrát rozhodujeme intuitívne, na základe emócií. Rozhodovanie si často zjednodušujeme a nedokážeme z dvoch možností vybrať tú výhodnejšiu. To má potom za následok mnoho rozhodnutí v živote, ktoré nie sú optimálne.
Pasívne investovanie je spôsob ako nenechať emóciám priestor, aby ovplyvňovali naše rozhodnutia v otázke budovania majetku. Správne pochopenie, ako funguje pravdepodobnosť jednotlivých javov, má zásadný vplyv na odstránenie emócií z investovania.
Čo nás vie naučiť teória pravdepodobnosti ohľadom správnych investičných rozhodnutí?
Zoberme si nasledujúce situácie a sami zodpovedzte, pre ktorú z možností by ste sa rozhodli:
Kotrú možnosť si vyberiete?
Ktorú možnosť si vyberiete?
K výsledkom sa vrátime ku koncu článku.
Čo všetko je potrebné brať do úvahy pri rozhodovaní, ak poznáme pravdepodobnosti výskytu určitého javu?
Existujú 3 základné koncepty, ktoré súvisia s praktickým uplatňovaním pravidiel pravdepodobnosti pri hrách, pri investovaní ale i pri rôznych životných situáciách, ktoré sa bežne dejú okolo nás.
Pri klasickom prístupe k teórii pravdepodobnosti sa pri jej skúmaní začínalo s analýzou základných hier, pri ktorých je rovnaká pravdepodobnosť určitého výsledku, ako napríklad pri hode mincou alebo kockou.
Napríklad pri hode kockou môže nastať 6 rôznych výsledkov s rovnakou pravdepodobnosťou, keďže kocka má 6 rôznych strán. Potom pravdepodobnosť, že hodíme kockou a padne zrovna jedno konkrétne číslo, závisí od počtu, koľkokrát sa toto číslo na kocke vyskytuje a počtu strán kocky.
Pravdepodobnosť toho, že na kocke padne napríklad číslo 2, je jedna ku šiestim. Kocka má 6 strán a číslo 2 je na nej zobrazené iba v jednom prípade.
Vo všeobecnosti môžeme konštatovať, že ak nejaká hra má n rovnako pravdepodobných výsledkov, z ktorých každý môže nastať v m prípadoch, tak pravdepodobnosť takéhoto javu sa vyjadruje ako pomer týchto dvoch premenných.
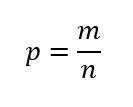
Túto úvodnú definíciu pravdepodobnosti však môžeme ďalej rozvíjať. Pravdepodobnosť nastania určitého javu sa približuje k určitej hodnote – limite, ktorá je vyjadrená ako podiel počtu ,koľkokrát tento jav nastal, k celkovému počtu pokusov.
Ak hodíme kockou šesťkrát, tak očakávame, že číslo 2 padne raz. Častokrát sa však stane, že pri šiestich hodoch číslo 2 padne aj viackrát. Pri šiestich hodoch kockou môže dvojka padnúť pokojne i 2-krát, 3-krát a v extrémnych prípadoch aj napríklad 6-krát.
Ak však pokus opakujeme dostočne veľakrát za sebou, tak číslo 2 padne približne toľkokrát, koľko by sme očakávali pri klasickej definícii pravdepodobnosti.
Pri mnohých pokusoch potom pravdepodobnosť definujeme ako limitu očakávanej pravdepodobnosti pri narastajúcom počte pokusov

Ak kockou hodíme desaťtsíckrát, tak počet padnutých dvojek bude blízko k jednej šestine z celkového počtu pokusov, konkrétne to bude niekde „blízko“ čísla 1667.
Druhou dôležitou ideou, ktorá súvisí s rozhodovaním na základe pravdepodobností, je koncept matematického očakávania.
Matematické očakávanie je vážený priemer náhodných premenných a dá sa matematicky vyjadriť nasledujúcim vzorcom
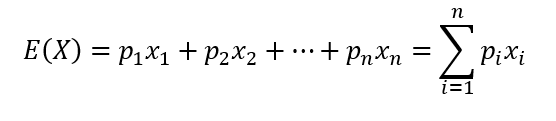
Matematické očakávanie náhodnej premennej X je súčet hodnôt, ktoré môže X dosiahnuť vynásobené pravdepodobnosťou, s akou môže daná hodnota nastať. Po súčte všetkých hodnôt dostaneme vážený priemer očakávaného výsledku.
Tento koncept je dôležitý i pri investovaní. Celkový výsledok každej investície ovplyvňujú ich denné zmeny, ktoré sú náhodnými premennými v čase a ktoré môžu mať rôzne hodnoty, plusové či mínusové.
V prípade hodu kockou tiež vieme dosiahnuť záporný výsledok, pokiaľ by sme pri hre uskutočnili vklad na naše číslo, a to číslo by nepadlo. Existujú však aj iné hry, kedy reálne strácame pri negatívnom výsledku, napríklad pri rulete.
Matematické očakávanie každej stávky vypočítame vynásobením každého možného výsledku, zvlášť pre pozitívny a zvlášť pre negatívny výsledok, s pravdepodobnosťou s akou môže nastať. Následne ich sčítame

Očakávanie z takejto hry sa rovná pravdepodobnosti zisku vynásobenej daným ziskom plus pravdepodobnosti straty vynásobenej danou stratou.
Ukážme si na konkrétnom príklade, ako by takéto matematické očakávanie mohlo vyzerať v prípade stávky na konkrétnu farbu pri americkej rulete.
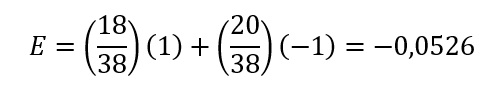
Ak pri americkej rulete stavíte na jednu farbu, napríklad červenú, tak vyhráte v 18-tich prípadoch z 38 možných (americká ruleta obsahuje aj zelené čísla 0 a 00, pri ktorých nevyhráva nikto). Prehráte v 20-tich prípadoch z 38 možných výsledkov. Matematické očakávanie takejto hry je negatívne. Konkrétne pri každej stávke môžete očakávať, že v priemere stratíte 5,26% z vašich peňazí.
Ďalšou z dôležitých vlastností matematického očakávania je jeho aditivita. Pri opakovaných viacnásobných stávkach pri rulete má každá z nich svoje vlastné matematické očakávania. Vaše celkové matematické očakávanie, teda váš celkový očakávaný výsledok po všetkých stávkach, bude jednoducho súčet jednotlivých očakávaní pri jednotlivých stávkach. Môžeme to vyjadriť nasledovným vzorcom
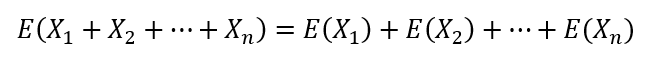
Z uvedených skutočností vyplýva, že ak chcete dosiahnuť dlhodobý očakávaný zisk pri stávkach, napríklad pri rulete, tak celkový súčet očakávaní pre jednotlivé stávky musí byť pozitívny.
Posledným z konceptov, ktoré majú veľký vplyv pri aplikácii teórie pravdepodobnosti do praxe, je Zákon veľkých čísiel.
Ten nám hovorí, že s narastajúcim počtom pokusov alebo stávok sa očakávaný pomer súčtu výsledkov k celkovému počtu pokusov približuje k očakávanému výsledku.
Keď sa pozrieme na priemerný výsledok stávok v rulete, vidíme, že sa s narastajúcim počtom pokusov sa celkový výsledok približuje k očakávanému výsledku. V našom prípade je to k hodnote -5,26%.
V obrázku vidíme, ako pri 100 náhodných simuláciách priebehu 100 stávok alebo hier v rulete priebežný dosiahnutý výsledok konverguje k matematicky očakávanému výsledku. Čím ďalej hráme, tým viac sa pokusmi približujeme k teoretickej hodnote. V prípade 100 hier je však vidno, že stále dostatočný počet výsledkov je nad hodnotou nula a nie je vizuálne jednoznačné, že takáto hra má negatívne matematické očakávanie.
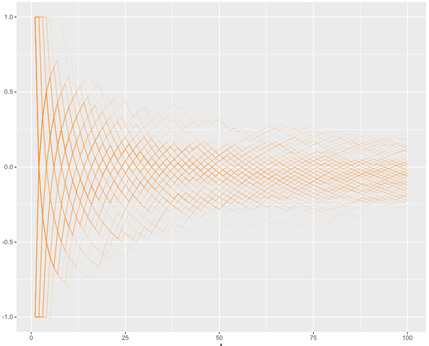
Ak však pokračujeme v hraní rulety ďalej, tak pribúdajúce priemerné výsledky sa ďalej zhlukujú pod nulovou hodnotou a je čím ďalej tým viac jasnejšie, že stredná hodnota očakávaného výsledku bude negatívna. Táto skutočnosť sa dá pozorovať na ďalšom obrázku pri 1000 uskutočnených ruletových hrách v 100 náhodných simuláciách.
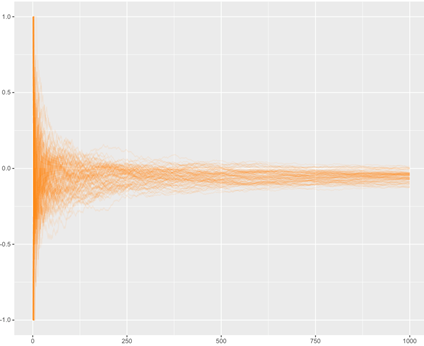
S pokračujúcim nárastom hier sa čoraz väčší počet priemerných výsledkov vyskytuje okolo hodnoty -0,0526. Pri 10000 hrách sa stredná hodnota výsledkov ustaľuje v okolí tejto hodnoty, ako naznačuje ďalší obrázok, a potvrdzuje tým negatívne matematické očakávanie.

Teraz môžeme všetky 3 koncepty spojiť dohromady a použiť ich pri analýze konkrétneho príkladu.
Prostredníctvom pravdepodobnosti dokážeme matematicky zanalyzovať náhodné javy pri rôznych hrách alebo stávkach. Aditívna vlastnosť matematického očakávania prináša možnosť výpočtu celkového očakávaného výsledku opakujúcich sa hier alebo stávok. Zákon veľkých čísiel nám zároveň zabezpečuje, že konečný výsledok série stávok bude konvergovať k očakávanému výsledku.
Negatívne matematické očakávanie nemusí nevyhnutne znamenať, že v danej hre budeme hneď od začiatku neúspešní. Vzhľadom na uvedené fakty je skôr dôležitý časový rámec, ako dlho hráme.
Aj pri hre s negatívnym matematickým očakávaním dokážeme v krátkodobom horizonte dosiahnuť kladný výsledok. Ak máme šťastie!
Skúsme sa pozrieť, aké sú možné scenáre vývoja hry pri rulete pri 100 stávkach v 100 simuláciách.

Zelené čiary zobrazujú cestu ku konečnému výsledku, ktorý bol kladný. Oranžové čiary zobrazujú cestu k zápornému výsledku po 100 stávkach.
Intuitívne sa zdá, že pri nie príliš veľkom počte opakujúcich sa hier sú naše šance na úspech približne 50:50. Stále vidíme dostatočný počet zelených čiar v porovnaní s oranžovými.
Vidíme, že mnohé z hier skončili skutočne s pozoruhodne kladným výsledkom, pričom najvyššia výhra je +26 (pri výhre zaknihujeme +1, pri prehre -1). Najvyššia prehra je niekde na úrovni -40.
Ak máme šťastie pri hre s negatívnym matematickým očakávaním, tak dokážeme v krátkodobom časovom horizonte dosiahnuť aj pozitívny výsledok. Je to tak aj z pohľadu dlhodobej hry?
Skúsme si to overiť pri pokračovaní vsádzania na jednu farbu pri rulete a pozrime sa na výsledky, aké by sme dosiahli po 1000 hrách v 100 simuláciách.
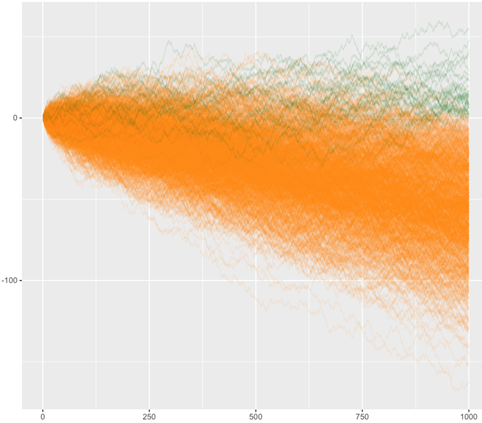
Pri 1000 hrách sa však už naša vidina úspešného konca v kasíne začína rozplývať. 100 simulácii vývoja nám naznačuje, že napriek zopár kladným výsledkom, veľká väčšina simulácii bola stratová.
Najlepší výsledok bol stále pozoruhodných +52, avšak najväčšia strata dosiahla až -160. Po 1000 simuláciách je už viac menej jasné, kam mieri celkový výsledok experimentu. Pri ďalšom pokračovaní hry sa pravdepodobne dostaneme do oveľa viac negatívneho teritória.
Negatívne matematické očakávanie pri rulete (z pohľadu hráča) sa s narastajúcim počtom opakovaní hry naplňuje (samozrejme, že z pohľadu kasína je opačné).
Pozrime sa ešte, či je tomu skutočne tak, ak budeme pokračovať v hre aj naďalej a zostaneme pri stole počas 10000 hier.

V stovke simulácií 10000 stávok pri americkej rulete vidíme, že nie je žiadna šanca, aby sme po takomto dlhom stávkovaní odišli od stola s pozitívnym výsledkom.
Očakávaný výsledok je v rozmedzí -150 až -870. Čím ďalej budeme pokračovať, tým horšie pre nás. Nie je riešením zostať pri stole dlhšie a veriť v obrat. Negatívne matematické očakávanie v kombinácii so Zákonom veľkých čísiel hrá nekompromisne v náš neprospech a dlhšia hra bude iba prehlbovať výsledkovú agóniu.
Aká je teda najlepšia stratégia pri americkej rulete?
Najlepšie je ju nehrať vôbec. Ak už predsa len hráte a náhodou ste v pluse, tak sa treba zodvihnúť a ísť preplatiť žetóny. Čím dlhšie budete ruletu hrať, tým väčšia je šanca, že sa vaše šťastie obráti a vy odídete domov so stratou.
Vráťme sa teraz k príkladu zo začiatku článku.
Pri prvej otázke si väčšina vyberie istotu a chce 20 EUR bez ohľadu na výsledok hodu mincou. Pozrime sa však na matematické očakávanie jednotlivých možností:
1.a. E = (0,5)(50) + (0,5)(0) = 25 EUR
1.b. E = (1)(20) + (0)(0) = 20 EUR
Prvé riešenie má väčšie matematické očakávanie ako druhé. Z krátkodobého hľadiska sa zdá byť lepším riešením brať istotu 20 EUR. Z dlhodobého hľadiska ak sa rozhodujete takýmto spôsobom, tak celkom isto prichádzate o finančné prostriedky.

Uskutočnili sme 1000 simulácií, kde sme porovnali možné výsledky. Zelené čiary predstavujú simuláciu priebehu výsledkov, ak si zakaždým vyberieme možnosť a), modrá čiara ukazuje vývoj, ak si zakaždým vyberieme možnosť b). Pri možnosti b) čiara lineárne rastie vždy o 20 EUR.
Už po 250 opakovaniach možnosti a) vidíme, že všetky možné scenáre vývoja sú nad modrou čiarou výsledku b). Výhodnosť voľby a) je však viditeľná počas celého priebehu pokusu. S narastajúcim počtom pokusov by sa výhodnosť riešenia a) iba zväčšovala, keďže vzdialenosť zeleného spektra výsledkov od modrej čiary by bola čoraz väčšia.
Zákon veľkých čísiel vám pri mnohých opakovaniach zabezpečí oveľa väčší benefit, ak budete brať do úvahy matematické očakávania jednotlivých udalostí. Pri opakovaní takýchto alebo podobných rozhodnutí je lepšie najskôr dôkladne zhodnotiť pravdepodobnosti a ekonomický prínos jednotlivých riešení v dlhodobom horizonte.
Pozrime sa na výsledky pri druhej otázke:
2.a. E = (0,5)(-50) + (0,5)(0) = -25 EUR
2.b. E = (1)(-20) + (0)(0) = -20 EUR
Je to zrkadlovo otočený príklad ako pri prvej otázke, avšak väčšina ľudí sa v tomto prípade rozhodne pre prvú možnosť. Ľudia sú citliví na okamžité straty a radšej podstúpia riziko, ak vidia možnosť sa im nejakým spôsobom vyhnúť.

Ekonomickejšie by však v tomto prípade bolo zvoliť možnosť b), keďže matematické očakávanie výsledku v peňažnom vyjadrení je v tomto prípade priaznivejšie. Po 250 pokusoch je modrá čiara nad celým oranžovým spektrom výsledkov z možnosti a).
Ďalším zaujímavým výsledkom z oboch príkladov je fakt, že pokiaľ ide o zisky, tak sme skôr náchylní ich vyberať čo najskôr, bez ohľadu na alternatívy.
Podobne ako v predchádzajúcich príkladoch funguje aj pasívne investovanie v dlhodobom horizonte.
V krátkom čase môže štandardná odchýlka spôsobiť, že investovanie do indexových fondov ETF je menej predpovedateľné. Ak však túto investíciu držíme dlhodobo, tak zákon veľkých čísiel a konvergencia k strednej hodnote matematického očakávania bude pôsobiť čím ďalej tým výraznejšie na kladné zhodnotenie.
Čas väčšinou hrá proti nám a sťažujeme sa na jeho nedostatok. Pri investovaní to však neplatí. Čím viac času poskytneme pasívnemu investovaniu, tým lepší výsledok môžeme očakávať.
Niekedy však niet času nazvyš.